C++ 归并排序

归并排序本身的思路很容易理解，也很适合用递归实现，但递归实现有缺陷，就是会有栈溢出的风险，递归深度有限。递归能实现的都可以转换成迭代实现，迭代实现其实就是把分解的步骤省了。

查了网上归并排序迭代的实现，很多都是 left_min、 left_max、 right_min、 right_max，然后 right_min 跟 left_max 都指向左部分的最后一个元素， right_max 则是指向右部分的最后一个元素的下一个位置，我觉得这样 min 和 max 的指向前后不一致，增加理解成本，所以下面的实现尽量保证不出现这样的问题，主要是避免日后回顾时看得费劲。

迭代实现

#include <iostream>
#include <vector>
using namespace std;

void MergeSort(vector<int>& vec);
void Print(const vector<int>& vec);

int main()
{
    vector<int> vec = { 49, 38, 65, 97, 76, 13, 27, 49 };
    cout << "before sort:" << endl;
    Print(vec);
    cout << "sort:" << endl;
    MergeSort(vec);
    cout << "after sort:" << endl;
    Print(vec);
}

void MergeSort(vector<int>& vec)
{
    int length = vec.size();
    vector<int> temp(length);
    for( int i = 1; i < length; i *= 2 )    //i代表待归并部分的元素个数，其他详解见1️⃣
    {
        int l;      //left，初始时指向左部分的第一个元素
        int le;     //left_end，指向左部分的最后一个元素
        int r;      //right，初始时指向右部分的第一个元素
        int re;     //right_end，指向右部分的最后一个元素
        int t;      //temp，指向temp的第一个元素
        int te;     //temp_end，指向temp的最后一个元素

        for( l = 0; l < length - i; l = re + 1 )   //2️⃣
        {
            le = l + i - 1;                     //3️⃣
            r = le + 1;
            re = min(r + i - 1, length - 1);
            t = l;                              //t保留l的初始值
            te = l;                             //te用来移动，指向最后一个元素

            while( l <= le && r <= re )         //l移动到le后面，即l>le，说明左部分元素都已经排进temp了，r同理
            {
                if( vec[l] <= vec[r] )          //注意是包含等于，保证了稳定性
                {
                    temp[te++] = vec[l++];
                }
                else
                {
                    temp[te++] = vec[r++];
                }
            }

            //可能出现其中一部分已经全部排进temp内，而另一部分还有剩余的情况

            while( l <= le )                    //左部分有剩余，将剩余的依次放进temp
            {
                temp[te++] = vec[l++];
            }

            while( r <= re )                    //同理，但其实右部分有剩余可以不进行处理留在原地，详解见4️⃣
            {
                temp[te++] = vec[r++];
            }

            while( te > t )                     //将temp保存的排好序的元素依次赋值回原容器
            {
                te--;
                vec[te] = temp[te];
            }
        }

        Print(vec);
    }
}

void Print(const vector<int>& vec)
{
    for( int v : vec )
    {
        cout << v << " ";
    }
    cout << endl;
}

1️⃣ for( int i = 1; i < length; i *= 2 )

• i 代表待归并的部分的应有元素个数， i=1 就是1个元素和1个元素进行归并， i=2 就是2个元素和2个元素进行归并。

  为什么说是应有元素个数，因为最后一份是可能不够数量的，例如一共3个元素 [1,2,3] ，当 i=2 时，就会是 [1,2] 和 [3] 。

• i<length ，因为如果 i=length ，那么第一部分有全部的元素，第二部分零个元素，那就没有归并的意义，或者说已经排完了。

2️⃣ for( l = 0; l < length - i; l = re + 1 )

• l 指向左部分的第一个元素，re 指向右部分的最后一个元素，所以 re+1 就是下一个左部分的第一个元素。

• l<length-i
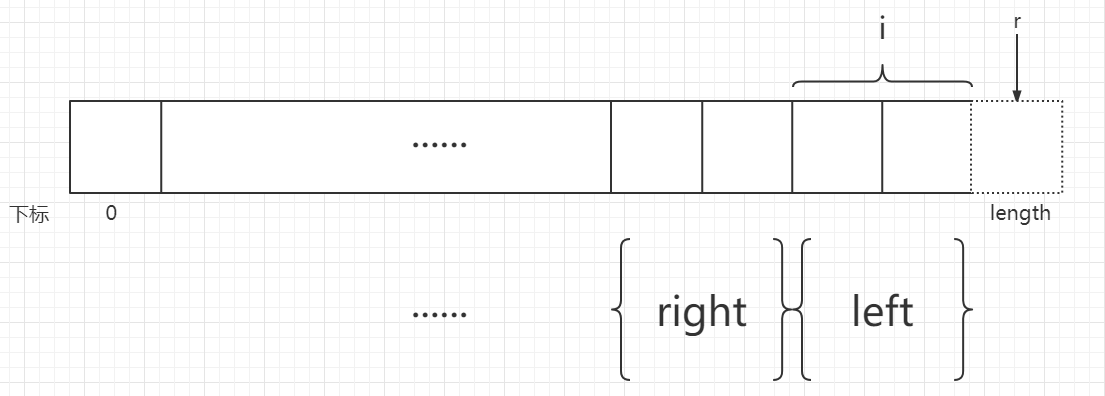
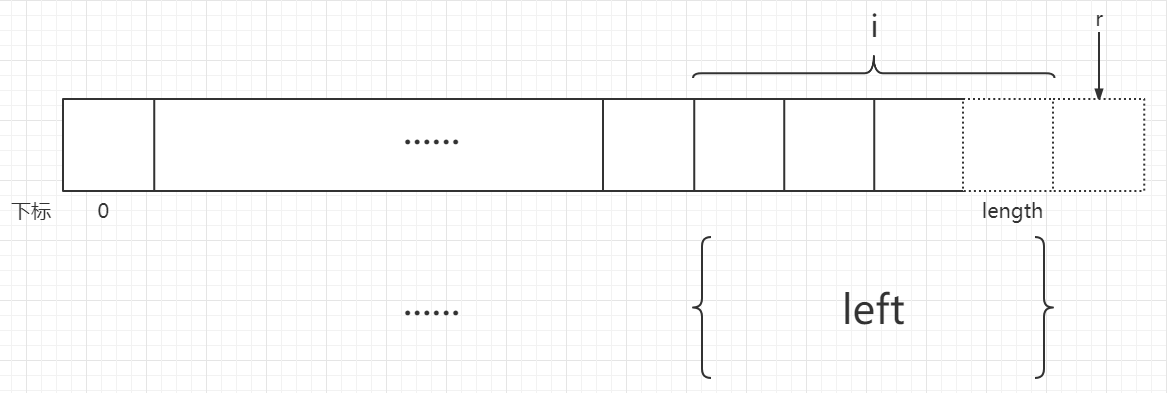
  首先想一想退出循环的条件，当什么时候应该退出循环呢，是不是当只有左部分而没有右部分的时候呢，因为需要有两个部分才能进行归并，退一步说，只有左部分时也进行归并，那么它该和谁归并呢，显然没有意义，所以当只有左部分时就应该退出循环。该情况下，设定 r 是右部分的第一个元素，如果左部分是满 i 个元素的话， r=length，见图0，如果左部分不满 i 个元素，那么 r>length，见图1，所以 r>=length。而 r=l+i，所以 l+i>=length，也就是 l>=length-i 的时候应该退出循环，即 l<length-i 是循环条件。

3️⃣ le = l + i - 1; r = le + 1; re = min(r + i - 1, length - 1);

• le = l + i - 1;
  l+i 指向右部分的第一个元素，所以 l+i-1 指向的就是左部分的最后一个元素。

• r = le + 1;
  上面的 le 指向左部分的最后一个元素，所以 le+1 就是右部分的第一个元素，也可以直接写 l+i。

• re = min(r + i - 1, length - 1);
  同理 r+i 指向下一个左部分的第一个元素，所以 r+i-1 指向的就是右部分的最后一个元素。

  但这是右部分能凑齐当前i数量元素的情况下，凑不齐的情况下，re 就只能指向容器的最后一个元素，无论右部分有几个元素。

  le、 r 为什么不需要考虑这个问题，因为该层循环的条件是 l<length-i，这个取值范围的前提就是肯定有右部分，le、r就一定不会越界。

4️⃣ while( r <= re ){ temp[te++] = vec[r++]; }

因为说明剩余的就是两部分中最大的几个元素，而且已经有序，放进 temp 中，等下也是原样赋值回来，为了一致，方便理解，还是保留了。